「冥王星、ハートマークくっきり」
2015年にニュー・ホライズンズが冥王星に最接近しました。
接近する際に撮影した写真に鮮明に「ハートマーク」が写っていた写真は、世界中の新聞にも掲載されました。
冥王星(pluto)というと死者の世界をつかさどる神の名前ですので、なんだか陰気なイメージがありましたが、「ハートマーク」効果のおかげでかなり印象が変わったのではないでしょうか。
ところで、冥王星の軌道は海王星の軌道の内側に入り込んでいることがわかっています。
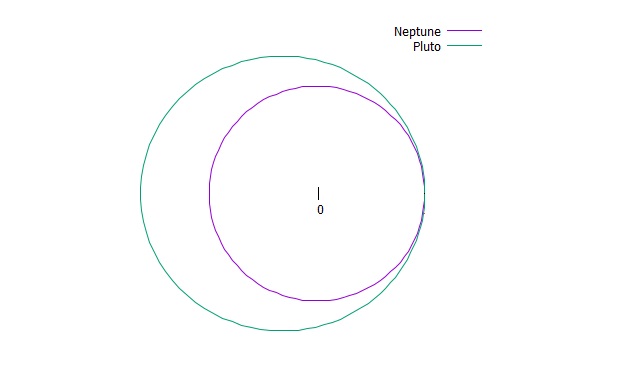
冥王星と海王星の軌道の略図
この軌道が分かってから、冥王星は海王星に衝突してしまう可能性があるのではないかと考える人もいました。
シミュレーションを行った結果、冥王星は海王星に大接近することなく、現在の軌道を回り続けるということが分かっています。
冥王星の公転周期は約248年で、海王星の公転周期は約165年です。
この公転周期の比を計算すると、
248/165 = 1.50
すなわち、冥王星が1周する間に海王星は1.5周します。
きれいに整数に直すと(すなわち、それぞれ2倍すると)、冥王星が2周する間に海王星は3周するのです。
この関係が、冥王星が海王星に衝突しない結果を引き起こしているのです。
海王星が冥王星に接近する場所を簡単なイメージで探ってみましょう。
小学生の時に
「池の周りを回っている人がいて、同じ向きに進む2人が追い越すのはどこ?」
という問題をやったことありませんか?
旅人算という名前がついているようですが、これを実際にやってみようというわけです。
今回はイメージを分かっていただきたいので、海王星の速度と冥王星の速度はそれぞれ一定とみなして考えます。
実際には楕円形の形をしていますが、軌道についてもほぼ円軌道の形とします。
イメージは次の通りです。
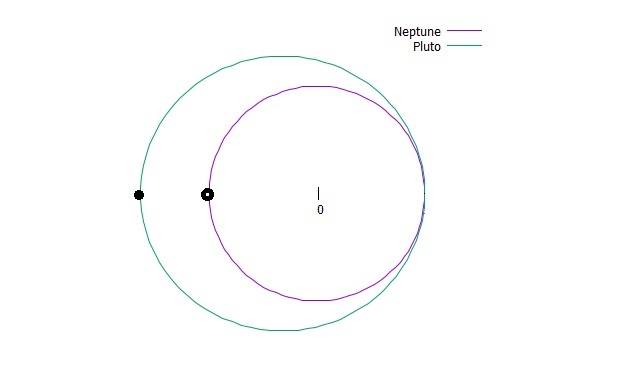
冥王星と海王星のスタート位置(黒丸)※冥王星の遠日点付近がスタート
図のように冥王星と海王星の軌道が最も離れているところからスタートさせます。
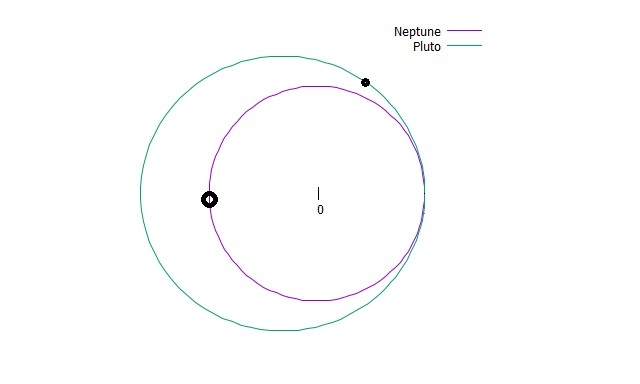
1.海王星が1周した時点で、冥王星はまだ2/3周しかしていません。
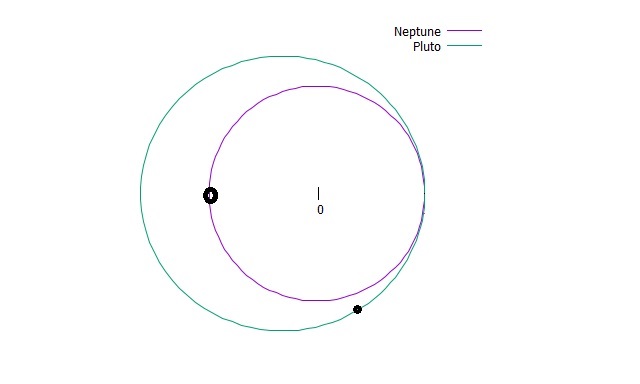
2.海王星が2周した時点で、冥王星は1と1/3周進みました。海王星が冥王星に追いついてきました。
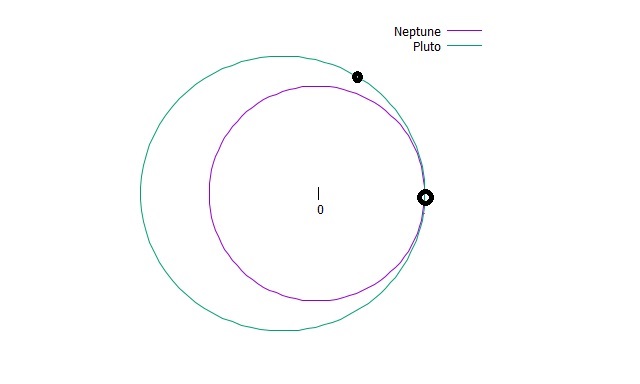
3.海王星が2と1/2周した時点で、冥王星は1と2/3周進みました。冥王星が海王星の軌道の内側に入り込んでいる部分に海王星がきたときには、冥王星はすでにその位置から離れています。

4.海王星が3周した時点で、冥王星は2周しました。海王星が追いついた位置は、冥王星と海王星の軌道が最も離れた場所です。
海王星は必ず同じ場所(冥王星の遠日点付近)で冥王星を追い越すのです。
これは何回やっても同じ結果になります。
実際に紙に書いて動かしてみると理解できると思います。
最初の冥王星と海王星の置いた位置が不自然?
という疑問がわくかもしれません。
確かに不自然に感じますよね・・・。
でも、現実にはこれが正しい冥王星と海王星の位置関係なのです。
海王星が3周回ったときに冥王星が2周回るという関係は、
必ず同じ場所で海王星が冥王星を追い越すことを意味している
という事実に注目してください。
例えば、冥王星と海王星の軌道が入れ替わっている図の右側からスタートしたとします。
そうすると、海王星が冥王星を追い抜く位置は必ずスタートした位置になります。
つまり、冥王星と海王星は非常に接近するのです。
巨大惑星に近づくとその引力を受けて軌道が変化することを意味しています。
そして、冥王星はどこかに行ってしまうか、海王星に衝突するでしょう。
逆に言えば、冥王星はたまたま現在の位置にあったので、今でもあるのです。
実際には海王星も冥王星も太陽を一つの焦点としただ円軌道を描いていますので、場所によって速度が異なります。
海王星はだ円軌道と言ってもほとんど円に近い軌道のため、遠日点での速度は近日点での速度の0.98倍です。
有効数字を小数点第1位とすると、遠日点と近日点の速度の差はないと考えてもいいでしょう。
それに対し、冥王星は少し潰れただ円のため、遠日点での速度は近日点での速度の0.6倍です。
もう少し改良したシミュレーションをするには、海王星が半周したときの冥王星の位置は1/3周よりも手前の位置にプロットさせます。
そして、海王星が1周したときの冥王星の位置を2/3周よりも進んだ位置にプロットすることで解決します。
この場合でも海王星が3周目に入った時に冥王星を後ろから追いかける位置になります
けれども、冥王星は近日点付近(海王星の軌道の内側に入り込んでいる部分)で速度が速くなりますので、まるで海王星から逃げるようにして近日点を通過する様子が描けます。
本格的なシミュレーションは、太陽、海王星、冥王星の三つの天体の万有引力による運動方程式の数値計算を行います。
数値計算については、大学で計算物理学の講義があるかと思いますので、そちらで学ぶとよいでしょう。
今回話題にした冥王星ですが、2006年に惑星から準惑星に「降格」したことでも有名です。
冥王星の近辺に小惑星がたくさんあることから、惑星の定義には当てはまらなくなってしまい、降格してしまったのです。
新しい発見はうれしいことですが、なんだか複雑な感じですね。
今回は冥王星についてのお話でしたが、太陽系外縁部の研究や系外惑星の研究を行っている研究室のある大学は、
- 東北大学
- 筑波大学
- 茨城大学
- 埼玉大学
- 東京大学
- 東京工業大学
- 京都大学
- 大阪大学
- 神戸大学
- 九州大学
- 兵庫県立大学(西はりま天文台 少人数受け入れ)
です。
















