高校物理では、二体問題:二つの物体の運動についてのみ学びます。
実際の正解では、いくつもの物体の運動をしている現象が多々あります。
実は、三体以上の物体の運動については、数学の知識を使って解くことが非常に困難なことが知られています。
でも、三体問題って解くことができるって聞いたこと、ありませんか?
ここでは、三体問題についてのお話をいたします。
二体問題の例
高校物理の力学では、二体問題:二つの物体の運動ついて学びます。
ボールを投げたときの運動はボール一つのみしか描かれていないのですが、相方は地球です。大きすぎて書けないだけです。
問題を解く時に「重力加速度: \(g\) 」を使うということは、暗黙のうちに地球が関与していることを意味しています。
地球がボールを引っ張る力が働いて「下」にボールが落ちるのです。(※1)
※1 気になる場合には、質量 \(m\) のボールと質量 \(M\) 、半径 \(R\) 地球との間に働く万有引力: \(F\) を使って、運動方程式: \(ma = F\) を立てて加速度 \(a\) を求めてみるといいでしょう(万有引力定数: \(G\) 、ボールの高さはせいぜい数メートルなので、地球の半径 \(R\) に比べて非常に小さいので無視できる高さ)。
三体問題の一般解は?
高校物理では、三体問題:三つの物体の運動については学びません。
これはカリキュラムの時間が足りないから教えないのではなく、二つの物体の運動を解く時のように運動方程式を立てても、求める変数18個に対して方程式の数が10個しかないため(この事実は証明済み)、一般解が求められないのです。
変数の数はある手法であと2個消すことができ、全部で16個になるのですが、それでもあと6個の方程式が足りないので、一般解は求められません。
※方程式があと六つ必要になるまで減らす過程については、「力学II 原島 鮮 裳華房」のP.124-P.128に記載されています。なお、ここでは大学で習う「解析力学」の知識を用いています。
もし授業で出てきて、一般解の解答を書くことになったら、
君 :「先生、問題が解けません! 教えてください。」
先生:「先生も解けないのです。」
君 :「・・・。」
何のために問題を出したのか分からなくなります・・・。
三体問題の一般解を求めなさいという問題は、高校のテストでは出ませんのでご安心を。
三体問題の解を調べる方法
しかし、その三体問題はあることをすれば解くことができる場合があります。
一つは近似を使う方法です。
例えば、太陽・木星・小惑星の運動を考えます(一般的には、第三の天体が他の二つの天体に比べて質量が圧倒的に小さい場合の運動になります)。
太陽は太陽系の中で一番重い星です。次に重いのが木星。小惑星は太陽や木星に比べたらずっと軽い星です。
三つの天体の運動方程式を立てると、小惑星が太陽や木星に与える引力はごくわずかです。小惑星の引力が太陽や木星の軌道に影響を与えるほど大きくありません。
そこで、小惑星の質量のみ0として問題を解こうという手法があります。これを
制限三体問題
と言います。
実はこのような条件をつけても一般解は求められないのですが、大局的な運動に関する情報が分かります。
この制限問題で見つかった解の中で有名なものは、トロヤ群と呼ばれる小惑星のグループです。木星の前後60度付近にあって、木星とほぼ同じ軌道を回っています。
数学の問題だと思っていたら、実際にそこに小惑星があったという事実は衝撃的だったようです。※2
※2 物理の世界では、方程式から導かれる解から予言できることについては、しばしば練習問題と見なされることがあります。ブラックホールも相対性理論から予言されていましたが、つい最近まで理論上の産物と見なされていました。
今では、ブラックホール同士の合体による重力波の検出もされて、存在が実証されています。2018年には、ついにブラックホールを直接撮影することができました!
先のトロヤ群に位置する二つの特殊解(正三角形平衡解)の他にも三つの特殊解が存在し、これらは直線平衡解と呼ばれています。
この二つの正三角形平衡解と3つの直線平衡解を合わせた五つの解を、ラグランジュ点と呼んでいます。
計算機が発達していなかった昔は、この五つの特殊解が知られていました。※3
※3 でも、私たちに最も近い恒星:ケンタウルス座α星は、3つの恒星がお互いを回っていますよね。以外に忘れがちですが、これも特殊解です。
最近は、コンピューターを使った数値計算(シミュレーション)により、より多くの特殊解がわかってきました。
三体問題は一般解が求められないのですが、方程式そのものは分かっています。つまり、ある条件(初期条件)を与えてあげれば、その方程式は解くことができるのです。これを特殊解と言います。
次に最初に求めた方程式の解を初期条件にして、少し時間を進めたときの解を求めます。
これを次々と計算していって、最終的にどのようになるかをシミュレーションにするのです。
最近は、コンピューターの性能が格段に良くなっていますので、このシミュレーションを使った研究も盛んになっています。
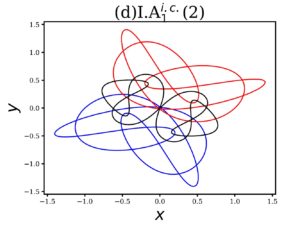
三体問題の安定軌道の例(Xiaoming LI, Yipeng JING, and Shijun LIAO 2018 (PASJ) Fig.1 より引用)
2018年には、1223個もの安定軌道を見つけたという論文も発表されています。
しかし、コンピューターの性能が格段に向上したため、N個の微惑星の引力の影響を全て考慮した計算もすることができますが、それでも計算するのに時間がかかります。
そこで、ある近似を用いて計算いたします。
惑星形成学やロケットの軌道計算では、中心にある恒星の周りを回る微惑星の運動を考えるときに使う近似があります。
Hill近似
と呼ばれるものです。これは、
- 微惑星の運動は、微惑星円盤の半径方向、垂直方向に居所的に考える。
- 二つの微惑星の重力相互作用は、かなり接近したときのみ、中心星の重力に比べて効果的である。
という近似です(これは微惑星のお話ですが、Hill方程式は量子力学における結晶中の電子の挙動解析にも応用されています)。
つまり、微惑星は、中心星の周りをケプラー運動をしていますが、二つの微惑星が接近したときのみ、お互いの重力の影響を受けるというものです。
最近では、重力以外の効果を入れた方程式で議論されることもあります(特に人工衛星関連)。
※地球惑星科学12 比較惑星学 岩波書店(ハードカバー版、新装版とも絶版)第3章P.193-P.197(ハードカバー版と新装版がありますが、どちらも同じページにあります。なお、新装版には補章として「小惑星」が10ページ追加されています。
天体力学という名前で講義を行っている大学は少ないのですが、名前は違っても二体問題や三体問題(N体問題)は、天文学以外でも重要な要素ですので、大学の講義のどこかで学ぶかと思います。
ただ、天体力学そのものは大学で学ぶ数学や物理の知識も必要としますので、まずは高校の数学と物理をマスターしましょう。
天体力学に関する日本の本は、出版されてもすぐに絶版になり、手に入りにくいです。
大学生の参考文献としてよくあげられている書籍は、「天体の位置と運動[第2版]」です。
ただ、大学レベルの数学が分かっているものとして話を進めていますので、式を追うのが難しいかもしれません。
式の展開をより丁寧に書いてある本は、「天体力学入門(4(1)」です。
(1)と書かれていますが、タイトルは(上)になっています。元々上下巻2巻構成でした。
上巻は、二体問題について書かれています。大学生で習うような数学もありますが、それについては解説をいれていますので、式の導出などがわかるようになっています。
天体力学の基本について知りたい場合にはこちらの本がおすすめです。
大学数学を使っている部分もありますが、式の展開がわかりやすいので、高校生の君でも頑張れば、この本を読むことができるかと思います。
次々と絶版になり、天体力学として扱っている日本の書籍はめっきり少なくなってしまいましたが、「天体力学入門」の書籍に記載されているレベルに近い書籍としては、次の書籍の第3章から第6章が近いものになります。
2018/01/18追記:
下巻で使われている摂動論ですが、第11章で正準変換と呼ばれる手法を用いています。
この書籍が発行された後のテキストを見ると、第9章の定数変化法を用いた摂動論で展開されています。
もし、下巻にチャレンジする場合には、ひとまず第9章までを目標にするといいでしょう。
その後、こういう方法もあるということを知る意味で、残りの章にチャレンジしてもいいですね。
2021/9/11追記:
残念ながら「天体力学入門(上)」も絶版になり、在庫も底をつきたようです。図書館に蔵書としてあることもあるので、興味のある方は、図書館で借りて学習するのもよいでしょう。
















